Answer:
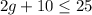
Explanation:
Given
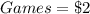 per game
per game
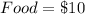
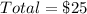 at most
at most
Required
Represent using an inequality
Represent the number of games with g
So, if 1 game costs $2,
g games would cost $2 * g
Since, I will be spending on games and food, my spending can be calculates as:
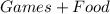
From the question, we understand that total spending is at most $25.
The term at most means

So, the expression can be represented as:
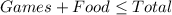
This gives:
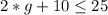
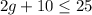
The above inequality models the scenario