Question

Take a trip to the bowling alley, where each game cost $2plus you plan to spend $10 on food. You can spend at most $25. Which inequality models this scenario?

Answer 1

`2g + 10 \leq 25`

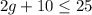
Explanation:

Given

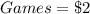`Games = \$2` per game

`Food = \$10`

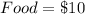
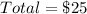`Total = \$25` at most

Required

Represent using an inequality

Represent the number of games with g

So, if 1 game costs $2,

g games would cost $2 * g

Since, I will be spending on games and food, my spending can be calculates as:

`Games + Food`

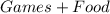
From the question, we understand that total spending is at most $25.

The term at most means
`\leq`

So, the expression can be represented as:

`Games + Food \leq Total`

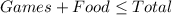
This gives:

`2 * g + 10 \leq 25`

`2g + 10 \leq 25`

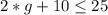
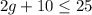
The above inequality models the scenario