Answer:
The earning rate is approximately 0.08.
Explanation:
We can determine the yearly rate by means of compound interest, which is defined by:
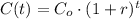 (Eq. 1)
(Eq. 1)
Where:
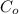 - Initial deposit, measured in US dollars.
- Initial deposit, measured in US dollars.
 - Earning rate, dimensionless.
- Earning rate, dimensionless.
 - Earning periods, measured in years.
- Earning periods, measured in years.
We proceed to clear the earning rate within:

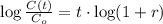
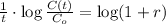
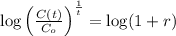
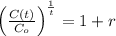
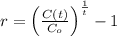
If we know that
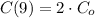 and
and
 , then the earning rate is:
, then the earning rate is:
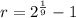
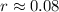
The earning rate is approximately 0.08.