Answer:
The magnitude of the ball's initial velocity is approximately 13.468 meters per second.
Step-by-step explanation:
From Trigonometry we get that magnitude of the velocity is obtained from the following trigonometric relation:
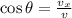 (Eq. 1)
(Eq. 1)
Where:
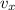 - Magnitude of the horizontal component of the baseball, measured in meters per second.
- Magnitude of the horizontal component of the baseball, measured in meters per second.
 - Magnitude of the velocity of the baseball, measured in meters per second.
- Magnitude of the velocity of the baseball, measured in meters per second.
 - Angle of baseball above the horizontal, measured in sexagesimal degrees.
- Angle of baseball above the horizontal, measured in sexagesimal degrees.
Then, we clear the magnitude of the velocity of the baseball:
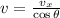
If we know that
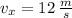 and
and
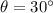 , then the magnitude of the velocity of the baseball is:
, then the magnitude of the velocity of the baseball is:
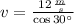
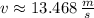
The magnitude of the ball's initial velocity is approximately 13.468 meters per second.