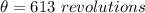Question

The angular speed of an automobile engine is increased at a constant rate from 1120 rev/min to 2560 rev/min in 13.8 s. (a) What is its angular acceleration in revolutions per minute-squared

Answer 1

Complete Question

The angular speed of an automobile engine is increased at a constant rate from 1120 rev/min to 2560 rev/min in 13.8 s.

(a) What is its angular acceleration in revolutions per minute-squared

(b) How many revolutions does the engine make during this 20 s interval?

rev

Answer:

a

`\alpha = 6261 \ rev/minutes^2`

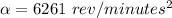
b

`\theta = 613 \ revolutions`

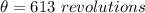
Step-by-step explanation:

From the question we are told that

The initial angular speed is
`w_i = 1120 \ rev/minutes`

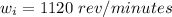
The angular speed after
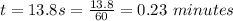`t = 13.8 s = (13.8)/(60 ) = 0.23 \ minutes` is
`w_f = 2560 \ rev/minutes`

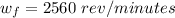
The time for revolution considered is
`t_r = 20 \ s = (20)/(60) = 0.333 \ minutes`

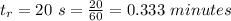
Generally the angular acceleration is mathematically represented as

`\alpha = (w_f - w_i )/(t)`

=>
`\alpha = (2560 - 1120 )/(0.23)`

=>
`\alpha = 6261 \ rev/minutes^2`

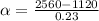
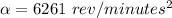
Generally the number of revolution made is
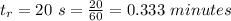`t_r = 20 \ s = (20)/(60) = 0.333 \ minutes` is mathematically represented as

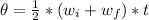
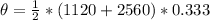
`\theta = (1)/(2) * (w_i + w_f)* t`

=>
`\theta = (1)/(2) * (1120+ 2560 )* 0.333`

=>
`\theta = 613 \ revolutions`