Question

De acuerdo con la tercera ley de movimiento planetario de Kepler, la masa de un planeta es directamente proporcional al cubo de la distancia promedio entre él y un satélite en órbita, pero inversamente proporcional al cuadrado del período orbital del satélite. La Tierra tiene una masa de 75.97×10^24 kg y está a una distancia promedio de 3.84×10^5 km de la Luna, la cual completa una órbita en 27.3 días. Si la Tierra orbita al Sol en 365.3 días y está a una distancia promedio de 1.496×10^8 km, ¿cuál es la masa del Sol?

Answer 1

La masa del Sol es
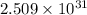`2.509* 10^(31)` kilogramos.

Explanation:

Tras una lectura cuidadosa al enunciado, tenemos que la Tercera Ley de Kepler queda descrita por la siguiente relación:

`M \propto (r^(3))/(T^(2))`

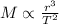
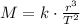`M = k\cdot (r^(3))/(T^(2))` (Eq. 1)

Donde:

`r` - Distancia entre los centros del planeta y el satélite, medido en kilómetros.

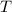`T` - Período oribital del satélite, medido en días.

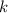`k` - Constante de proporcionalidad, medida en kilogramo-días cuadrados por kilómetro cúbico.

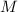`M` - Masa del planeta, medida en kilogramos.

Podemos obtener la masa del Sol mediante la siguiente relación:

`(M_(S))/(M_(E)) = ((r_(E)^(3))/(T_(E)^(2)) )/((r_(M)^(3))/(T_(M)^(2)) )`

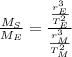
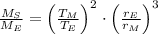`(M_(S))/(M_(E)) = \left((T_(M))/(T_(E)) \right)^(2)\cdot \left((r_(E))/(r_(M)) \right)^(3)` (Eq. 2)

Donde:

`T_(M)`,
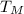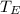`T_(E)` - Períodos orbitales de la Luna y la Tierra, medidos en días.

`r_(E)`,
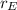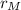`r_(M)` - Distancias entre la Tierra y el Sol, así como entre la Luna y la Tierra, medidas en kilómetros.

`M_(S)`,
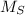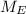`M_(E)` - Masas del Sol y la Tierra, medidos en kilogramos.

Si
`M_(E) = 75.97* 10^(24)\,kg`,
`T_(E) = 365.3\,d`,
`T_(M) = 27.3\,d`,
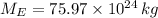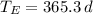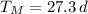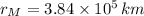`r_(M) = 3.84* 10^(5)\,km` y
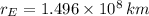`r_(E) = 1.496* 10^(8)\,km`, entonces tenemos que la masa del Sol es:

`M_(S) = \left((T_(M))/(T_(E)) \right)^(2)\cdot \left((r_(E))/(r_(M)) \right)^(3)\cdot M_(E)`

`M_(S) = \left((27.3\,d)/(365.3\,d) \right)^(2)\cdot \left((1.496* 10^(8)\,km)/(3.84* 10^(5)\,km) \right)^(3)\cdot (75.97* 10^(24)\,kg)`

`M_(S) = 2.509* 10^(31)\,kg`

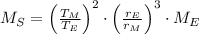
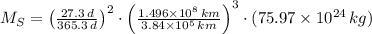
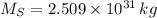
La masa del Sol es
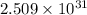`2.509* 10^(31)` kilogramos.