Question

A vector makes an angle, theta, with the horizontal. The horizontal and vertical components of the vector will be equal in magnitude if the angle theta is

1 point
a.90°
b.60°
c.45°
d.30°

Answer 1

c. 45°

Step-by-step explanation:

Answer 2

The correct option is;

c. 45°

Step-by-step explanation:

The given information is that the angle the vector makes with the horizontal = θ

Let the magnitude of the resultant vector = R

The horizontal component of the vector are given as follows;

Rₓ = R × cos(θ)

The vertical component of the vector are given as follows;

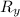`R_y` = R × sin(θ)

The resultant vector, R, in vector form, R, is the sum of the horizontal and vertical components as follows;

R = R × cos(θ)·i + R × sin(θ)·j

Therefore;

The horizontal and vertical component will be equal when cos(θ) = sin(θ)

Given that tan(θ) = sin(θ)/cos(θ), we have that when cos(θ) = sin(θ), tan(θ) = sin(θ)/cos(θ) = sin(θ)/sin(θ) = 1

tan(θ) = 1,

∴ θ = tan⁻¹(1) = 45°

θ = 45°.