Question

The function g(x) = 12,500(0.91)x represents the value of a piece of farm equipment after x years. Approximately when will its value be half its original value?

A.
8.1 years

B.
7.3 years

C.
4.6 years

D.
3.9 years

Answer 1

B. 7.3 years

Explanation:

The question is wrong. The correct function is :

`g(x)=12500(0.91)^(x)`

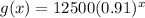
We have the function
`g(x)` that represents the value of a piece of farm equipment after
`x` years.

This means that when
`x=0` its original value is :

`g(0)=12500(0.91)^(0)=12500`

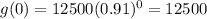
Now we want to calculate approximately when will its value be half its original value. Then, we write :

`(12500)/(2)=6250`

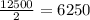
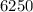`6250` is half of its original value. We need to find
`x` that satisfies the following equation :

`g(x)=6250=12500(0.91)^(x)`

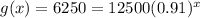
Solving for
`x` :

`6250=12500(0.91)^(x)` ⇒

`0.5=(0.91)^(x)`

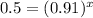
Now we apply natural logarithm to each side of the equation :

`ln(0.5)=ln[(0.91)^(x)]`

Using logarithm properties :

`ln(0.5)=ln[(0.91)^(x)]` ⇒

`ln(0.5)=x[ln(0.91)]`

`x=(ln(0.5))/(ln(0.91))` ⇒

`x` ≅
`7.3496`

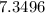
The correct option is B. 7.3 years