Question

The parabola y = -(x − 3)² + 6 has its focus at (3,1). Determine and state the equation 20 of the directrix.​

Answer 1

well, tis noteworthy that the equation of the parabola above is already in vertex form, which means its vertex is at (3 , 6) and its focus point is at (3 , 1).

now, the focus point is below the vertex, meaning is a vertical parabola opening downwards, like a hump.

`\textit{vertical parabola vertex form with focus point distance} \\\\ 4p(y- k)=(x- h)^2 \qquad \begin{cases} \stackrel{vertex}{(h,k)}\qquad \stackrel{focus~point}{(h,k+p)}\qquad \stackrel{directrix}{y=k-p}\\\\ p=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix}\\\\ \stackrel{`

`y=-\cfrac{1}{20}(x-3)^2+6\implies y-6=-\cfrac{1}{20}(x-3)^2\implies \stackrel{4p}{-20}(y-\stackrel{k}{6})=(x-\stackrel{h}{3})^2 \\\\\\ 4p=-20\implies p=-\cfrac{20}{4}\implies p=-5`

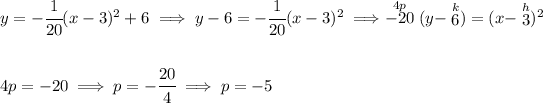
the focus point must be a negative distance since the parabola is opening downwards, and the directrix is across the vertex at "p" distance, Check the picture below.