well, tis noteworthy that the equation of the parabola above is already in vertex form, which means its vertex is at (3 , 6) and its focus point is at (3 , 1).
now, the focus point is below the vertex, meaning is a vertical parabola opening downwards, like a hump.

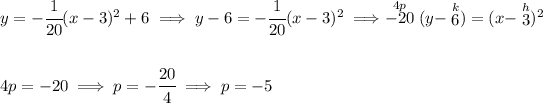
the focus point must be a negative distance since the parabola is opening downwards, and the directrix is across the vertex at "p" distance, Check the picture below.