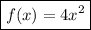Question

Determine whether a quadratic model exists for each set of values. If so, write the model.

f(-2)=16, f(0)=0, f(1)=4

Answer 1

`f(x)=4x^2`

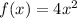
Explanation:

Quadratic Model

The quadratic function can be expressed in the form:

`f(x)=ax^2+bx+c`

Where a,b, and c are constants to be determined using the points through which the function passes.

We have the points (-2,16) (0,0) (1,4). To find the values of a,b,c we just substitute the values of x and y and solve the system of equations.

Point (0,0):

`f(0)=a*0^2+b*0+c=0`

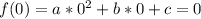
It follows that

c=0

Point (-2,16):

`f(0)=a*(-2)^2+b*(-2)+c=16`

Operating:

`a*(4)+b*(-2)+c=16`

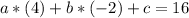
Since c=0:

`4a-2b=16`

Divide by 2:

`2a-b=8\qquad\qquad [1]`

Point (1,4):

`f(1)=a*(1)^2+b*(1)+c=4`

`a*(1)+b*(1)+c=4`

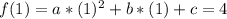
Since c=0:

`a+b=4\qquad\qquad [2]`

Adding [1] + [2]:

2a+a=12

3a=12

a=12/3=4

a=4

From [2]

b=4-a

b=4-4=0

b=0

The model is:

`\boxed{f(x)=4x^2}`