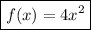Answer:
Explanation:
Quadratic Model
The quadratic function can be expressed in the form:
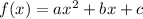
Where a,b, and c are constants to be determined using the points through which the function passes.
We have the points (-2,16) (0,0) (1,4). To find the values of a,b,c we just substitute the values of x and y and solve the system of equations.
Point (0,0):
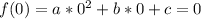
It follows that
c=0
Point (-2,16):
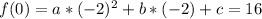
Operating:
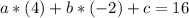
Since c=0:
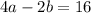
Divide by 2:
![2a-b=8\qquad\qquad [1]](https://img.qammunity.org/2021/formulas/mathematics/college/v3pbu1lnn38168mz2dg3gbxszs178w8pix.png)
Point (1,4):
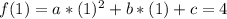
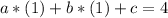
Since c=0:
![a+b=4\qquad\qquad [2]](https://img.qammunity.org/2021/formulas/mathematics/college/scd6v7pvmpxjyvrwjblacrv538vnhu9sxd.png)
Adding [1] + [2]:
2a+a=12
3a=12
a=12/3=4
a=4
From [2]
b=4-a
b=4-4=0
b=0
The model is: