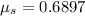Answer:
The coefficient of static friction is
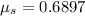
Step-by-step explanation:
From the question we are told that
The tangential acceleration is
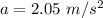
Generally the circumference of the circle is mathematically represented as
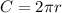
and given that the car travels one quarter of the circular path before it skids off the track , then the distance traveled along the track is mathematically represented as
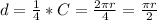
Generally from kinematic equations
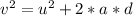
Here u is the initial velocity of the car which is 0 m/s
while v is the velocity of the car that keeps it from skiing off the track
So
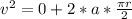
=>
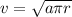
Generally the centripetal force acting on the car is mathematically represented as
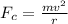
=>
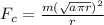
=>
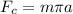
Generally the frictional force between the track and the tires of the car is mathematically represented as
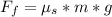
Generally the tangential force acting on the car is mathematically represented as
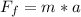
Generally the resultant force acting on the car is mathematically \
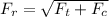
=>
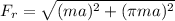
=>
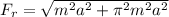
=>
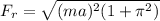
=>

Generally the point before the car skids off the track, frictional force is equal to the resultant force and this is mathematically represented as
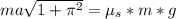
=>
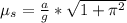
=>
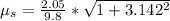
=>