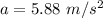Answer:
The acceleration is
Step-by-step explanation:
From the question we are told that
The mass of the weight is

The radius of the spool is
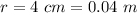
The mass of the spool is

Generally the net force acting on the weight is mathematically represented as
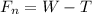
Here W is the weight of the weight which is mathematically represented as
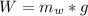
and T is the tension on the thread
So
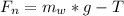
Generally this net force acting on the weight can be mathematically represented as
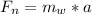
Here is the a is the acceleration of the system (i.e acceleration of the weight as a result of its weight and the tension on the rope )
So
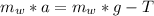
Generally the torque which the spool experiences can be mathematically represented as

This torque is also mathematically represented as
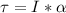
Here
 is moment of inertia of the spool which is mathematically represented as
is moment of inertia of the spool which is mathematically represented as
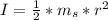
while
 is the angular acceleration of the spool which is mathematically represented as
is the angular acceleration of the spool which is mathematically represented as
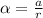
so
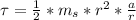
=>

So
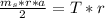
=>

Now substituting this formula for T into the equation above
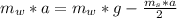
=>
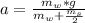
=>
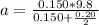
=>