Answer:
Ambos tienen la misma probabilidad de lograr su objetivo y esa probabilidad es 0.81
Explanation:
Se sabe que nuestra urna contiene bolas numeradas del 0 al 99. En total tenemos 100 bolas en nuestra urna.
Definimos los siguientes eventos :
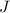: '' El número extraído no incluye en su numeración la cifra 3 ''
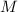: '' El número extraído no incluye en su numeración la cifra 9 ''
Para saber quién tiene mayor probabilidad de lograr su objetivo debemos calcular la probabilidad de los eventos
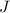y
.
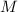Ahora bien, nuestro espacio muestral (Ω) está conformado por los siguientes elementos :
Ω = {0, 1 , 2 , ... , 99}
Donde cada uno de ellos tiene la misma probabilidad de ocurrencia. Estamos ante un espacio muestral equiprobable. Por ende, para calcular las respectivas probabilidades de los eventos
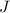y
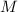vamos a hacerlo mediante la siguiente fórmula :
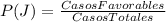
Los casos totales son 100 (es el número de bolas numeradas en la urna).
Los casos favorables al evento
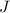son 81 (son todos los números del 0 al 99 que no incluyen la cifra 3 en su numeración) ⇒
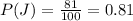
La probabilidad del evento
es 0.81
De manera análoga, calculamos la probabilidad del evento
:
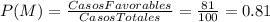
De igual manera, los casos totales siguen siendo 100.
Tenemos 81 números del 0 al 99 que no incluyen la cifra 9 en su numeración.
La probabilidad del evento
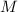es 0.81
La probabilidad de ambos eventos es igual y vale 0.81
Finalmente, tanto Juan como María tienen la misma probabilidad de lograr su objetivo.