Question

E

Graph the linear equations given the following details:
A. Using two points.
1. (2, -1) and (3, 2)
3. (4, 3) and (0, 5)
2.
(4, -2) and (-5, 2)
4. (1,6) and (-2,-5)
Find the slope of each line. Describe the graph.
B. Using intercepts
5.
(0, -3) and (1, 0)
7. (5,0) and (0, -4)
6.
(-3, 0) and (0, -3)
8. (2.0) and ( 0, 0, -4)
Find the slope of the line. Describe the graph.
c. Using slope and a point
9.
m = 5 and (6, -1)
11. m = - 2 and (4, 1)
10.
12. m = Hand
m =zand (2, -4)
5
Hand (-3,-3)
3​

Answer 1

A. Please see the attached graphs

B. 5. The equation of the graph is y = 3·x - 3

6. The equation of the graph is y = x + 3

7. The equation of the graph is y = 4/5·x - 4

8. The equation of the graph is y = 2·x - 4

9. The graph is the line with equation y = 5·x - 31

10. The graph is the line with equation y = 5·x - 14

11. The graph is the line with equation y = -2·x + 9

12. The graph is the line with equation y = 3·x + 6

Explanation:

A. Please see the attached graphs

B. 5. The intercepts are;

(0, -3) and (1, 0)

The slope is given by the following equation;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

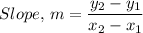
For the coordinate points, (0, -3) and (1, 0) we have;

m = (0 - (-3))/(1 - 0) = 3

The slope = 3

From the point and slope form, of a straight line equation, we have;

y - 0 = 3(x - 1)

The equation of the graph is therefore;

y = 3·x - 3

The y-intercept occurs at (0, -3)

The x intercept occurs where y = 0

0 = 3·x - 3

x = 3/3 = 1

The x-intercept occurs at (1, 0)

The graph of the equation, y = 3·x - 3, passes through the y and x intercepts (0, -3) and (1, 0) respectively

6. The coordinate points are;

(-3, 0) and (0, -3)

The slope is given by the following equation;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

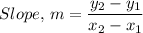
For the coordinate points, (-3, 0) and (0, -3) we have;

m = ((-3) - 0)/(0 - (-3)) = -1

The slope = 1

From the point and slope form, of a straight line equation, we have;

y - 0 = 1(x - (-3)) = x + 3

y = x + 3

The y-intercept occurs at (0, 3)

The x intercept occurs where y = 0

0 = x + 3

x = -3

The x-intercept occurs at (-3, 0)

The graph of the equation, y = x + 3, passes through the y and x intercepts (0, 3) and (-3, 0) respectively

7. The coordinate points are;

(5, 0) and (0, -4)

The slope is given by the following equation;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

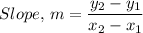
For the coordinate points, (5, 0) and (0, -4) we have;

m = ((-4) - 0)/(0 - 5) = 4/5

The slope = 4/5

From the point and slope form, of a straight line equation, we have;

y - 0 = 4/5×(x - 5) = -4/5·x - 4

y = 4/5·x - 4

The y-intercept occurs at (0, -4)

The x intercept occurs where y = 0

0 = -4/5·x + 4

-4 = -4/5·x

x = 5

The x-intercept occurs at (5, 0)

The graph of the equation, y = 4/5·x - 4, passes through the y and x intercept (0, 4) and (5, 0) respectively

8. The coordinate points are;

(2, 0) and (0, -4)

The slope is given by the following equation;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

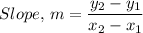
For the coordinate points, (2, 0) and (0, -4) we have;

m = ((-4) - 0)/(0 - 2) = 2

The slope =2

From the point and slope form, of a straight line equation, we have;

y - 0 = 2×(x - 2) = 2·x - 4

y = 2·x - 4

The y-intercept occurs at (0, -4)

The x intercept occurs where y = 0

0 = 2·x - 4

4 = 2·x

x = 2

The x-intercept occurs at (2, 0)

The graph of the equation, y = 2·x - 4 passes through the y and x intercept (0, -4) and (2, 0) respectively

C. Using the point and slope form

9. The slope m = 5 and the graph passes through the points (6, -1)

We have the point and slope form given as follows;

y - (-1) = 5·(x - 6)

y = 5·x - 30 - 1 = 5·x - 31

y = 5·x - 31

The graph is the line with equation y = 5·x - 31

10. The slope m = 5 and the graph passes through the points (2, -4)

We have the point and slope form given as follows;

y - (-4) = 5·(x - 2)

y = 5·x - 10 - 4 = 5·x - 14

y = 5·x - 14

The graph is the line with equation y = 5·x - 14

11. The slope m = -2 and the graph passes through the points (4, 1)

We have the point and slope form given as follows;

y - 1 = (-2)·(x - 4)

y = -2·x + 8 + 1 = -2·x + 9

y = -2·x + 9

The graph is the line with equation y = -2·x + 9

12. The slope m = 3 and the graph passes through the points (-3, -3)

We have the point and slope form given as follows;

y - (-3) = 3·(x - (-3))

y = 3·x + 9 - 3 = 3·x + 6

y = 3·x + 6

The graph is the line with equation y = 3·x + 6