Question

Please help quick!!
Given ΔΡHS & ΔCNF, find the values of x, y, and z.

Answer 1

`x=24, y=10, z=17`

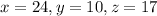
Explanation:

We know that
`\Delta PHS\cong\Delta CNF`.

Then by CPCTC, ∠P≅∠C, ∠H≅∠N, and ∠S≅∠F.

Therefore, let’s solve for each of the angle relations.

∠P≅∠C:

We know that ∠P is 36°. ∠C is (4z-32)°. Therefore:

`36=4z-32`

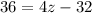
Solve for z:

`\begin{aligned}36&=4z-32\;\;\; \text{Add 32 to both sides}\\68&=4z\;\;\;\;\;\;\;\;\;\;\;\text{Divide both sides by 4}\\17&=z\end{aligned}`

So, the value of z is 17.

∠H≅∠N

∠H is (6x-29) and ∠N is 115. So:

`6x-29=115`

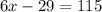
Solve for x:

`\begin{aligned} 6x-29&=115\;\;\;\;\;\;\text{Add 29 to both sides}\\6x&=144\;\;\;\;\;\;\text{Divide both sides by 4}\\\ x&=24\end{aligned}`

Therefore, the value of x is 24.

∠S≅∠F

We will need to find ∠S.

We already know that ∠P is 36.

∠H will be (6x-29). Substitute 24 for x to acquire: (6(24)-29)=144-29=115.

A triangle always totals 180°. Therefore, 115+36+∠S=180 or 151+∠S=180.

Therefore, ∠S=29.

∠F is (3y-1). So:

`29=3y-1`

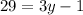
Solve for y:

`\begin{aligned} 29&=3y-1\;\;\;\;\;\text{Add 1 to both sides}\\ 30&=3y\;\;\;\;\;\;\;\;\;\;\text{Divide both sides by 3}\\ 10&=y\end{aligned}`

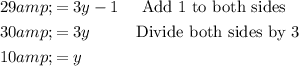
Therefore, the value of y is 10.

So, x=24, y=10, and z=17.

And we are done!