Answer:
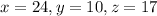
Explanation:
We know that
 .
.
Then by CPCTC, ∠P≅∠C, ∠H≅∠N, and ∠S≅∠F.
Therefore, let’s solve for each of the angle relations.
∠P≅∠C:
We know that ∠P is 36°. ∠C is (4z-32)°. Therefore:
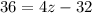
Solve for z:

So, the value of z is 17.
∠H≅∠N
∠H is (6x-29) and ∠N is 115. So:
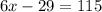
Solve for x:

Therefore, the value of x is 24.
∠S≅∠F
We will need to find ∠S.
We already know that ∠P is 36.
∠H will be (6x-29). Substitute 24 for x to acquire: (6(24)-29)=144-29=115.
A triangle always totals 180°. Therefore, 115+36+∠S=180 or 151+∠S=180.
Therefore, ∠S=29.
∠F is (3y-1). So:
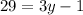
Solve for y:
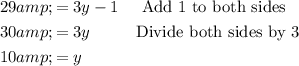
Therefore, the value of y is 10.
So, x=24, y=10, and z=17.
And we are done!