Question

How many solutions does this system of equations have?

y=x^2+x+3
y=-2x-5


A.
no solution
B.
1 solution
C.
2 solutions
D.
3 solutions

Answer 1

a. a a a a a a a a aa a. a a a a. a. a a

Answer 2

Answer: A. No solution

Explanation:

System of Equations

We have this system of equations:

`y=x^2+x+3`

`y=-2x-5`

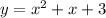
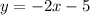
To solve the system, we can substitute y from one equation into the other:

`x^2+x+3=-2x-5`

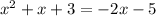
Prepare the second-degree equation. Adding 2x+5:

`x^2+x+3+2x+5=0`

Simplifying:

`x^2+3x+8=0`

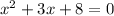
The equation has the coefficients:

a=1, b=3, c=8

To find out the number of real solutions of the quadratic equation, we calculate the discriminant d:

`d=b^2-4ac`

`d=3^2-4(1)(8)`

`d=9-32=-23`

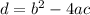
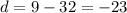
Since the discriminant is negative, the equation has no real solutions, thus the system of equations has no real solution.

Answer: A. No solution