Answer:
Answer: A. No solution
Explanation:
System of Equations
We have this system of equations:
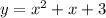

To solve the system, we can substitute y from one equation into the other:
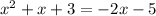
Prepare the second-degree equation. Adding 2x+5:

Simplifying:
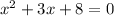
The equation has the coefficients:
a=1, b=3, c=8
To find out the number of real solutions of the quadratic equation, we calculate the discriminant d:


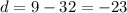
Since the discriminant is negative, the equation has no real solutions, thus the system of equations has no real solution.
Answer: A. No solution