Question

Please help asap i cannot find the answer anywhere.

Graph the system of inequalities presented here on your own paper, then use your graph to answer the following questions:

y < 4x − 8
y is greater than or equal to negative 5 over 2 times x plus 5

Part A: Describe the graph of the system, including shading and the types of lines graphed. Provide a description of the solution area.

Part B: Is the point (5, −8) included in the solution area for the system? Justify your answer mathematically.

Answer 1

• y<4x-8

< sign so it's dotted line to be graphed .

Put (0,0)

• 0<0-8
• 0>-8

Away from origin shading

And

• y≥-5/2x+5

Put 0

• 0≥-5/5=-1

Rational function ,two side parabola type lines

Dark lines and it's shading from origin in one part and in other towards origin(Look attachment)

Graph attached

Yes (5,8) is included in solution region

Answer 2

Given inequalities:

`y < 4x-8`

`y\geq -(5)/(2)x+5`

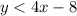
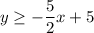
Part A

The graph of the system is made up of 2 straight line graphs.

The graph of
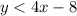`y < 4x-8` is a dashed straight line with shading under the line.

The graph of
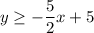`y\geq -(5)/(2)x+5` is a solid straight line with shading above the line.

The solution area is the area where the shading of the two lines overlaps.

Part B

To determine if the point (5, -8) is included in the solution area, input the point into both inequalities:

`\begin{aligned}y & < 4x-8\\\implies -8 & < 4(5)-8\\-8 & < 20-8\\-8 & < 12 \quad \leftarrow \textsf{correct}\end{aligned}`

`\begin{aligned}y & \geq -(5)/(2)x+5\\\implies -8 & \geq -(5)/(2)(5)+5\\\implies -8 & \geq -7.5 \quad \leftarrow \textsf{incorrect}\end{aligned}`

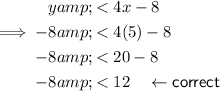
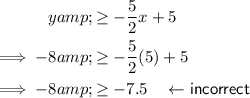
Therefore, the point (5, -8) is not included in the solution area as it is only true for one inequality.