Question

Which statement BEST explains the relationship between lines GF & HJ?

Answer 1

Option (4)

Explanation:

Slope a line passing through two points
`(x_1,y_1)` and
`(x_2,y_2)` is given by,

m =
`(y_2-y_1)/(x_2-x_1)`

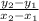
Since, blue line is passing through two points (-4, -2) and (0, 4),

Slope of the blue line =
`(4+2)/(0+4)`

=
`(3)/(2)`

Similarly, green line is passing through two points (-4, 1) and (0, -2),

Slope of the green line =
`(1+2)/(-4-0)`

=
`-(3)/(4)`

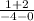
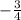
Since,
`(3)/(2)\\eq -(3)/(4)`

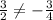
Neither these slopes are opposite reciprocals.

Therefore, both the lines are neither parallel nor perpendicular.

Option (4) will be the correct option.