Answer:
Option (4)
Explanation:
Slope a line passing through two points
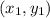 and
and
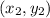 is given by,
is given by,
m =
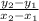
Since, blue line is passing through two points (-4, -2) and (0, 4),
Slope of the blue line =
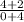
=
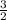
Similarly, green line is passing through two points (-4, 1) and (0, -2),
Slope of the green line =
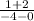
=
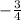
Since,
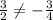
Neither these slopes are opposite reciprocals.
Therefore, both the lines are neither parallel nor perpendicular.
Option (4) will be the correct option.