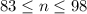Answer:
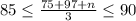 ;
;
Explanation:
Score of the first two quizzes: 75 and 97
Let n represent the third score
Average score would be:
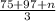 .
.
Given that the average score fall between 85 and 90, this can be represented by the compound inequality as shown below:
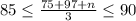
Solve for n in each statement that makes up the compound inequality:
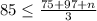

Multiply both sides by 3
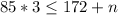
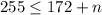
Subtract 172 from each side of the inequality
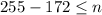

Also,
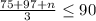
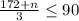
Multiply both sides by 3
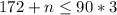
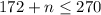
Subtract 172 from both sides of the inequality
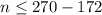

Combining both together, the possible values of her third quiz score would be: