Hello!
A)
We can solve for the reactances of each element using the following equations.
Capacitive reactance:
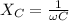
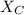 = Capacitive reactance (Ω)
= Capacitive reactance (Ω)
ω = Angular frequency (2000 rad/sec)
C = Capacitance (2 μF)
Plug in the given values and solve.
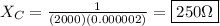
Inductive reactance:
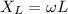
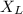 = Inductive reactance (Ω)
= Inductive reactance (Ω)
L = Inductance (70 mH)
Solve:
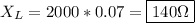
We can solve for impedance using the following equation:
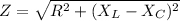
Z = Impedance (Ω)
R = Resistance (200Ω)
Find the impedance using the values above and the given resistance:
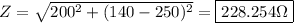
B)
The maximum current amplitude is found using Ohm's law:
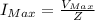
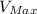 = 80V
= 80V
Z = 228.254 Ω
Solve.
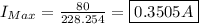
To find the max voltages across each element, we can also use Ohm's Law.
For the resistor:
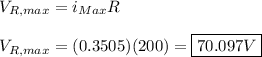
For the capacitor:
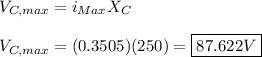
For the inductor:
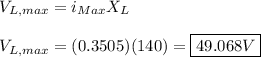
C)
The maximum voltage across each element is greater than 80 V because of the transfer of energy between the capacitor and inductor that occur at different times (energy is stored and released) and being in addition to the voltage of the power source.