Answer:
97.92 m³ (nearest hundredth)
Explanation:
The composite solid is a cube with a cone cut out.
Therefore, to find the volume of the solid, subtract the volume of the cone from the volume of the cube.
Volume of Cube

Given:
Substitute given value into the formula:

Volume of Cone

Given:
Substitute given values into the formula:
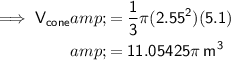
Volume of Composite Solid
