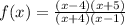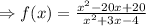Question

Write an equation for a rational function with:

Vertical asymptotes at x = -4 and x = 1

x intercepts at x = 4 and x = -5

y intercept at 5

y=

Preview

Dointe occible. 1

Answer 1

`f(x)=(x^2-20x+20)/(x^2+3x-4)`

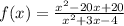
Explanation:

Let the fractional form of the function is

`f(x)= \frac {N}{D}\cdots(i).`

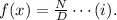
As there are two vertical asymptotes at x = -4 and x = 1

so, the denominator of the function must be 0 at x=-4 as well as x=1, so, (x+4) and (x-1) is factors of the denominator, D.

D=a(x+4)(x-1)

where a is constant.

As, at x intercepts at x = 4 and x = -5, so the function is zero at x=4 and x=-5.

So, (x-4) and (x+5) are the factors of numerator, so

N=b(x-4)(x+5), where b is a constant.

From the equation (i),

`f(x)=\frac {b(x-4)(x+5)}{a(x+4)(x-1)}\cdots(ii)`

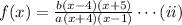
As y intercept is 5, so at x=0,

f(x=0)=5

`\Rightarrow \frac {b(0-4)(0+5)}{a(0+4)(0-1)}=5`

`\Rightarrow \frac b a * \frac {-20}{-4}=5`

`\Rightarrow \frac b a =1`

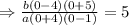
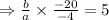
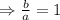
Put the value of
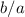`b/a` in equation (ii), the required rational function is

`f(x)=\frac {(x-4)(x+5)}{(x+4)(x-1)}`

`\Rightarrow f(x)=(x^2-20x+20)/(x^2+3x-4)`