Question

a toothpick is 3 inches long. troy has a box whose base is 1 inch x 1 inch. what is the shortest height possible for the box so that the toothpick fits entirely inside. round to the nearest hundredth

Answer 1

2.65 inches

Explanation:

The length of the toothpick is 3 inches.

The of the base of the box is 1 inch x 1 inch.

Let the height of the box is h inch, so, the dimension of the box is

1 inch x 1 inch x h inch.

The toothpick must be placed diagonally for the minimum height of the box, as shown in the figure,

So, the length of the longest diagonal of the box

`d=\sqrt {1^2+1^2+h^2}`

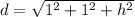
As the length of the toothpick is 3 inches, so d= 3

`\Rightarrow 3=\sqrt {2+h^2}`

`\Rightarrow 9=2+h^2`

`\Rightarrow h^2=9-2=7`

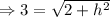
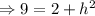
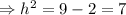
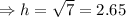`\Rightarrow h = \sqrt 7=2.65` inches.

Hence, the shortest possible length of the box is 2.65 inches.