Question

PLEASE HURRY According to a poll, 30% of voters support a ballot initiative. Hans randomly surveys 5 voters. What is the probability that exactly 2 voters will be in favor of the ballot initiative? Round the answer to the nearest thousandth.

P (k successes) = Subscript n Baseline C Subscript k Baseline p Superscript k Baseline (1 minus p) Superscript n minus k. Subscript n Baseline C Subscript k Baseline = StartFraction n factorial Over (n minus k) factorial times k factorial EndFraction

0.024

0.031

0.132

0.309

Answer 1

Option D) 0.309

Explanation:

Correct on edge

Answer 2

0.309

Explanation:

→ Utilise the binomial distribution formula

`p=nCr*p^(n) *q^(n-r)`

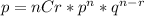
→ It first will be 5C2 as there is 5 possible voters but he wants 2 voters

`p=5C2*p^(n) *q^(n-r)`

→ Then it will be
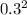`0.3^(2)` as the probability they are in favour is 0.3 and we get the n from the 2 number for the 5C2

`p=5C2*0.3^(2) *q^(n-r)`

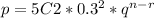
→ There for q will be 0.7 as it is the other probability left and the power will be 3 as it is n - r

`p=5C2*0.3^(2) *0.7^(3)`

→ Then getting 0.3087 which is 0.309