Question

For the function f ( x ) = − 2x^2 + 2x + 8 , evaluate and fully simplify each of the following.

f ( x + h ) =

f ( x + h ) − f ( x ) =

Answer 1

`f(x+h)=- 2x^2-4xh-2h^2 + 2x+2h + 8`

`f ( x + h ) - f ( x )= h(-4x-2h+2)`

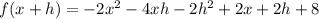
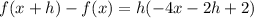
Explanation:

Given the function:

`f ( x ) = - 2x^2 + 2x + 8`

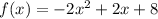
Find

• f ( x + h )
• f ( x + h ) - f ( x )

Recall the identity to square a binomial:

`(a+b)^2=a^2+2ab+b^2`

`f(x+h)=- 2(x+h)^2 + 2(x+h) + 8`

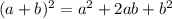
Squaring the binomial:

`f(x+h)=- 2(x^2+2xh+h^2) + 2(x+h) + 8`

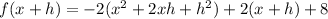
Multiplying:

`\boxed{f(x+h)=- 2x^2-4xh-2h^2 + 2x+2h + 8}`

--------------------------------------------------------------

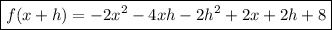
To compute f ( x + h ) - f ( x ), we use the last result:

`f ( x + h ) - f ( x )=- 2x^2-4xh-2h^2 + 2x+2h + 8-(- 2x^2 + 2x + 8)`

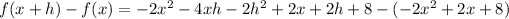
Multiplying:

`f ( x + h ) - f ( x )=- 2x^2-4xh-2h^2 + 2x+2h + 8+ 2x^2 - 2x - 8`

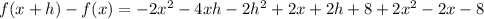
Simplifying similar terms:

`f ( x + h ) - f ( x )= -4xh-2h^2+2h`

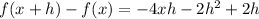
Factoring:

`\boxed{f ( x + h ) - f ( x )= h(-4x-2h+2)}`

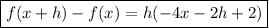
Note: This expression is commonly used to compute the first derivative of a function by its definition.