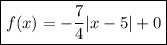Question

NO LINKS!!! Please help me with this graph. Part 6a​

Answer 1

`f(x) = -(7)/(4)|x-5|+0`

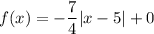
Step-by-step explanation:

The function in the coordinate Plane is an absolute value function . Consider the parent function

`f(x) = |x|`

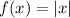
Recall the properties of transformation

• f(x+a), If a<0 ⇒ It moves to right
• a.f(x),If a<0 ⇒ It flips upsidedown
• f(x)+a,If a>0 ⇒ It moves up & a<0 It moves down

From the inspection of the graph,It has moved to right by 5 units, Thus

`f(x - 5) = |x - 5|`

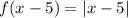
Apparently, It has neither shifted up or down, hence

`f(x - 5) +0= |x - 5|+0`

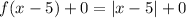
Looking at the graph, we can see that it has been reflected vertically. It tells us we have to multiply it by a negative constant

`-a f(x - 5) +0= -a |x - 5| +0`

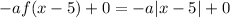
take (9,7) to figure out a.

• set x to 9 and the LHS expression to 7

`-a | 9- 5| =7`

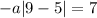
Solving the equation yields:

`\boxed{a = - (7)/(4) }`

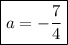
hence, our function is
`\boxed+0`

Answer 2

`\large{\boxed \ g(x) = -(7)/(4) }`

Step-by-step explanation:

Absolute value of a graph formula:

• y = a |x -h| + k

Identify the vertex : (h, k) = (5, 0)

Take two points : (5, 0), (9, -7)

`\sf Find \ slope \ (a) : \sf \ (y_2 - y_1)/(x_2- x_1) \ = \ (-7-0)/(9-5) \ = \ -(7)/(4)`

Join the variables together:
`\bf g(x) = - (7)/(4) | x -5| +0`