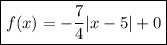Answer:
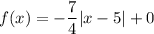
Step-by-step explanation:
The function in the coordinate Plane is an absolute value function . Consider the parent function
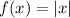
Recall the properties of transformation
- f(x+a), If a<0 ⇒ It moves to right
- a.f(x),If a<0 ⇒ It flips upsidedown
- f(x)+a,If a>0 ⇒ It moves up & a<0 It moves down
From the inspection of the graph,It has moved to right by 5 units, Thus
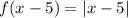
Apparently, It has neither shifted up or down, hence
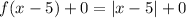
Looking at the graph, we can see that it has been reflected vertically. It tells us we have to multiply it by a negative constant
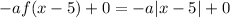
take (9,7) to figure out a.
- set x to 9 and the LHS expression to 7
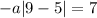
Solving the equation yields:
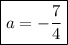
hence, our function is