Answer:
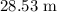
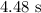

Step-by-step explanation:
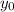 = Height from where the ball is thrown =
= Height from where the ball is thrown =
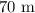
 = Angle of inclination =
= Angle of inclination =
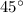
 = Initial velocity =
= Initial velocity =

 = Acceleration due to gravity =
= Acceleration due to gravity =
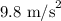
Range of projectile is given by
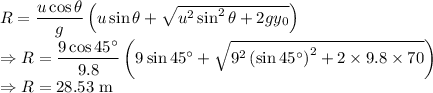
The ball will land
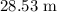 away.
away.
Time of flight is given by

The time the ball will stay in the air is
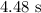
Maximum height is given by
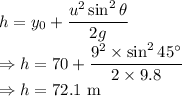
Maximum height the object will reach above the ground is
 .
.