Answer:

Explanation:
Given :
To find :
Solution :
Remember that the sum of complementary angles is always 90°.
First, finding the value of x :
Set up an equation :
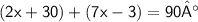 ( Being complementary angles )
( Being complementary angles )
Solve for x
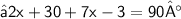 { Remove unnecessary parentheses }
{ Remove unnecessary parentheses }
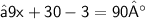 { Combine like terms }
{ Combine like terms }
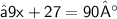 { Subtract 3 from 30 }
{ Subtract 3 from 30 }
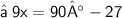 { Move 27 to right hand side and change it's sign }
{ Move 27 to right hand side and change it's sign }
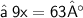 { Subtract 27 from 90}
{ Subtract 27 from 90}
 { Divide both sides by 9 }
{ Divide both sides by 9 }
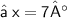
The value of X is 7°
Now, Replacing the value of x in order to find the value of
 B
B
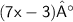
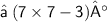 { Plug the value of x }
{ Plug the value of x }
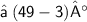 { Multiply 7 by 7 }
{ Multiply 7 by 7 }
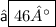 { Subtract 3 from 49 }
{ Subtract 3 from 49 }
The measure of
 B is 46°
B is 46°
And we're done!
Hope I helped!
Best regards! :D
~TheAnimeGirl