Question

ZA and ZB are complementary angles. If mZA= (2x + 30)° and m

ZB = (7x – 3)', then find the measure of ZB.

Answer 1

`\huge{ \boxed{ \bold{ \tt{46 \degree}}}}`

Explanation:

Given :

• 
  `\sf{m \angle \: A \: = \: (2x + 30)°}`
• 
  `\sf{ \: m \angle \: B \: = (7x - 3)°}`

To find :

• 
  `\sf{measure \: of \angle \: B} \: = ?`

Solution :

Remember that the sum of complementary angles is always 90°.

First, finding the value of x :

Set up an equation :

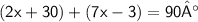`\sf{(2x + 30) + (7x - 3) = 90°}` ( Being complementary angles )

Solve for x

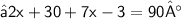`\sf{⇢2x + 30 + 7x - 3 = 90°}` { Remove unnecessary parentheses }

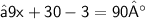`\sf{⇢9x + 30 - 3 = 90°}` { Combine like terms }

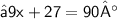`\sf{⇢9x + 27 = 90°}` { Subtract 3 from 30 }

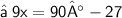`\sf{⇢ \: 9x = 90° - 27}` { Move 27 to right hand side and change it's sign }

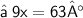`\sf{⇢ \: 9x = 63°}` { Subtract 27 from 90}

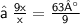`\sf{⇢ \: (9x)/(x) = (63°)/(9)}` { Divide both sides by 9 }

`\sf{⇢ \: x = 7°}`

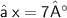
The value of X is 7°

Now, Replacing the value of x in order to find the value of
`\angle` B

`\sf{(7x - 3)°}`

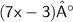
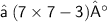`\sf{⇢ \: (7 * 7 - 3)°}` { Plug the value of x }

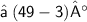`\sf{⇢ \: (49 - 3)°}` { Multiply 7 by 7 }

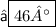`\sf{⇢ \boxed{46°}}` { Subtract 3 from 49 }

The measure of
`\angle` B is 46°

And we're done!

Hope I helped!

Best regards! :D

~TheAnimeGirl