Hi Student!
Looking at the problem, we first need to determine the important information that is given to us. We can see that we are given a radius of 6 feet and a central angle of 110 degrees. We will need to use both of these given values in our problem.
The second step that we need to take, after gathering our information, is to convert our degrees to radians. The purpose of this is because in our formula we must use radians instead of degrees. To convert degrees to radians, we multiply it by π/180.
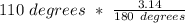

Now that we have our angle converted to radians, we can plug our information into the formula and solve.

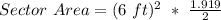

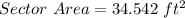
Therefore, after solving the entire equation down to the end, we can see that our answer is 34.542 feet squared. This matches option B which would be our answer.