Question

If the volume of a sphere is 256π/3 what is the radius?

Answer 1

4

Explanation:

The volume of a sphere is equal to 4/3πr³.

Set up the equation;

4/3πr³=256π/3

Multiple both sides by 3/(4π):

r³=64

r=∛64=4 (ans)

Answer 2

`\boxed {\boxed {\sf r=4}}`

Explanation:

The volume of a sphere is calculated using the following formula:

`v= (4)/(3) \pi r^3`

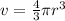
The volume of the sphere is
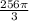`\frac {256 \pi}{3}`. Substitute this value in for v.

`(256 \pi)/(3) = (4)/(3) \pi r^3`

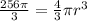
We are solving for the radius, so we must isolate the variable r. It is being multiplied by 4/3π. We can divide by this fraction or multiply by the reciprocal. The reciprocal is the fraction flipped, or 3/4π

`\frac {3}{4 \pi} *(256 \pi)/(3) = (4)/(3) \pi r^3 *\frac {3}{4 \pi}`

`\frac {3}{4 \pi} *(256 \pi)/(3) = r^3`

`64 =r^3`

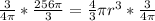
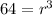
The variable is being cubed. The inverse of a cube is the cube root, so we take the cube root of both sides of the equation.

`\sqrt[3]{64}=\sqrt[3]{r^3}`

`\sqrt[3]{64}=r`

`4=r`

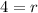
The radius of the sphere is 4.