Question

Chem help!! I know the answer is 8 but why?

Answer 1

Step-by-step explanation:

It's simple train track method of cancelling out units.

If we read the balanced equation as this: 2 dm3 of octane reacts to form 16 dm3 of CO2 then how much CO2 is produced by 1 dm3?

Would you agree that it would be half of 16?

`(2dm3)/(16 CO2) = (1dm3)/(?CO2)`

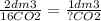
Cross multiply and solve for ?, you get 8.