Answer:
Step-by-step explanation:
It's simple train track method of cancelling out units.
If we read the balanced equation as this: 2 dm3 of octane reacts to form 16 dm3 of CO2 then how much CO2 is produced by 1 dm3?
Would you agree that it would be half of 16?
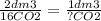
Cross multiply and solve for ?, you get 8.