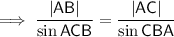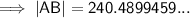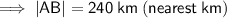Answer:
|AB| = 240 km (nearest km)
Explanation:
Draw a sketch with the given information (attached).
Calculate the missing angle (shown in red on the attached diagram).
Given:
The interior angles of a triangle sum to 180°
⇒ ∠ACB + ∠CAB + ∠CBA = 180°
⇒ ∠ACB + 27° + 66° = 180°
⇒ ∠ACB = 180° - 27° - 66°
⇒ ∠ACB = 87°
Use Sine Rule for sides to calculate |AB|:

(where A, B and C are the angles and a, b and c are the sides opposite the angles)