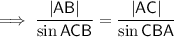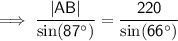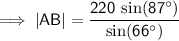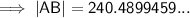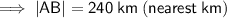Question

An aircraft is timetabled to travel from A to B. Due to bad weather it flies from A to C then from C to B, where AC and CB make angles of 27° and 66° respectively with AB. If |AC| = 220 km, calculate |AB|.​

Answer 1

|AB| = 240 km

Explanation:

Finding ∠C :

⇒ 27° + 66° + ∠C = 180°

⇒ ∠C = 180° - 93°

⇒ ∠C = 87°

Applying the Law of Sines :

⇒ sin 66° / 220 = sin 87° / AB

⇒ 0.913545458 / 220 = 0.998629535 / AB

⇒ AB = 220/0.913545458 x 0.998629535

⇒ AB = 240.819981 x 0.998629535

⇒ AB = 240.489946

⇒ |AB| = 240 km (nearest whole kilometer)

Answer 2

|AB| = 240 km (nearest km)

Explanation:

Draw a sketch with the given information (attached).

Calculate the missing angle (shown in red on the attached diagram).

Given:

• ∠CAB = 27°
• ∠CBA = 66°

The interior angles of a triangle sum to 180°

⇒ ∠ACB + ∠CAB + ∠CBA = 180°

⇒ ∠ACB + 27° + 66° = 180°

⇒ ∠ACB = 180° - 27° - 66°

⇒ ∠ACB = 87°

Use Sine Rule for sides to calculate |AB|:

`\sf (a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

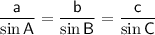
(where A, B and C are the angles and a, b and c are the sides opposite the angles)

`\implies \sf (|AB|)/(\sin ACB)=(|AC|)/(\sin CBA)`

`\implies \sf (|AB|)/(\sin (87^(\circ)))=(220)/(\sin (66^(\circ)))`

`\implies \sf |AB|=(220\:\sin (87^(\circ)))/(\sin (66^(\circ)))`

`\implies \sf |AB|=240.4899459...`

`\implies \sf |AB|=240\:km\:(nearest\:km)`