Answer:
The coordinates of the other endpoint are
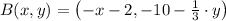 .
.
Explanation:
Let
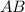 a line segment in which
a line segment in which
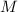 is the midpoint. If both
is the midpoint. If both
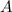 and
and
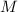 are given, then we determine the location of
are given, then we determine the location of
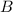 from definition of midpoint. That is:
from definition of midpoint. That is:
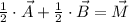 (Eq. 1)
(Eq. 1)
Where:
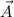 ,
,
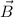 - Endpoints with respect to origin, dimensionless.
- Endpoints with respect to origin, dimensionless.
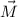 - Midpoint with respect to origin, dimensionless.
- Midpoint with respect to origin, dimensionless.
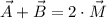
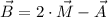
If we know that
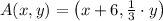 and
and
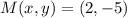 , then the coordinates of
, then the coordinates of
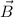 are:
are:
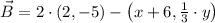
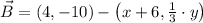
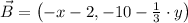
The coordinates of the other endpoint are
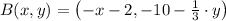 .
.