Question

The Australian sheep dog is a breed renowned for its intelligence and work ethic. It is estimated that 4 0% of adult Australian sheep dogs weigh 65 pounds or more. A sample of 1 4 adult dogs is studied. What is the standard deviation of the number of dogs who weigh 65 lb or more?

Answer 1

The standard deviation of the number of dogs who weigh 65 lbs or more is 1.83.

Explanation:

Let X represent the number of adult Australian sheep dogs weighing 65 pounds or more.

It is provided that the probability of occurrence of X is, p = 0.40.

A sample of n = 14 adult dogs is studied.

Each dog's weight is independent of the others.

The random variable X follows a Binomial distribution.

The standard deviation of a Binomial distribution is:

`\sigma=√(np(1-p))`

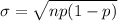
Compute the standard deviation of the number of dogs who weigh 65 lbs or more as follows:

`\sigma=√(np(1-p))`

`=√(14* 0.40(1-0.40))\\\\=√(3.36)\\\\=1.83303\\\\\approx 1.83`

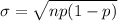
Thus, the standard deviation of the number of dogs who weigh 65 lbs or more is 1.83.