Question

The volume of a circular cylinder is calculated using the formula = ^2*2ℎ. If the height ℎ is known to be equal to the diameter 2 and ℎ is measured at a percentage error of 2%, find the percentage error in calculating the volume of the cylinder.

Answer 1

6%

Explanation:

From the information given:

The height h is said to be equal to the diameter which is 2r

h = 2r

r = h/2

Recall that: The volume for calculating a circular cylinder is:

`V = \pi r^2 h`

`V = \pi ((h)/(2))^2 h`

`V =(\pi h^3)/(2)`

`(dV)/(dh) = (3 \pi h^3)/(4)`

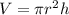
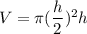
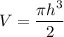
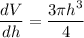
Thus, the percentage error of the height can now be calculated as:

`(dh )/(h) * 100 = 2`

`dh =(h)/(50)`

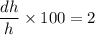
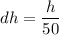
Now taking the differential of the volume, we have:

`dV = (dV)/(dh)* dh`

`dV = (3 \pi h^2)/(4)* (h)/(50)`

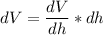
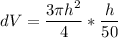
FInally, the %age change in the volume is calculated as follows:

`(dV)/(V) = ( (3 \pi h^2)/(4)* (h)/(50))/((\pi h^3)/(2))`

`(dV)/(V) = (3)/(50) * 100 \%`

`(dV)/(V) =6 \%`

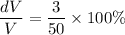
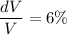
Thus; the percentage error in calculating the volume of the cylinder is 6%