Answer:
6%
Explanation:
From the information given:
The height h is said to be equal to the diameter which is 2r
h = 2r
r = h/2
Recall that: The volume for calculating a circular cylinder is:
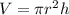
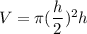
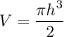
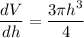
Thus, the percentage error of the height can now be calculated as:
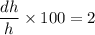
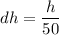
Now taking the differential of the volume, we have:
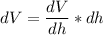
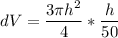
FInally, the %age change in the volume is calculated as follows:
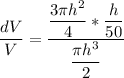
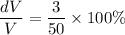
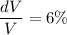
Thus; the percentage error in calculating the volume of the cylinder is 6%