Answer:
The point (-3,-5) is the solution of the system because it satisfies both equations
Explanation:
System of equations
A system of equations represents a situation where multiple conditions apply, and the possible solution to the system, if any, must satisfy all conditions, not just some of them.
We have the system of equations:
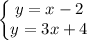
The solution of the system is an ordered pair (x,y) that satisfies both equations.
Test the point (-3,-5):
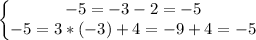
We can see both equalities are true, thus the point (-3,-5) is the solution of the system because it satisfies both equations