Question

Kristen deposited $9,000 in an account that has an annual interest rate at.  4.1% compounded monthly .how much interest will she earn at the end of one month ?show all work

Answer 1

$9,030.75

Step-by-step explanation:

S.I = P×R×T ÷ 100

=9000 (1×4.1%×)

Answer 2

Kristen will earn approximately $30.25 in interest at the end of one month with a 4.1% annual interest rate compounded monthly. This calculation is based on her $9,000 initial deposit using the compound interest formula.

Step-by-step explanation:

Kristen's interest can be calculated using the formula for compound interest:

`\[ A = P \left(1 + (r)/(n)\right)^(nt) \]`

where:

-
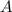`\( A \)`is the future value of the investment/loan, including interest,

-
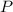`\( P \)`is the principal amount (initial deposit),

-
`\( r \)`is the annual interest rate (as a decimal),

-
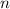`\( n \)` is the number of times that interest is compounded per unit
`\( t \)`(time in years), and

-
`\( t \)` is the time the money is invested/borrowed for in years.

In this case, Kristen's principal
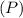`(\( P \))` is $9,000, the annual interest rate
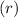`(\( r \))` is 4.1%, compounded monthly
`(\( n = 12 \))`, and
`\( t \)`is 1/12 since we're calculating for one month.

`\[ A = 9000 \left(1 + (0.041)/(12)\right)^{(12 \cdot (1)/(12))} \]`

Solving this equation yields the future value after one month, including interest. Subtracting the initial principal gives us the interest earned:

`\[ \text{Interest} = A - P \]`

After the calculations, the interest earned is approximately $30.25. This amount represents the interest Kristen will have accrued on her $9,000 deposit after one month, considering the compounded monthly interest rate of 4.1%.