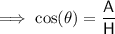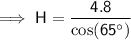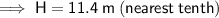Answer:
A) 7.1 m
B) 11.4 m
Explanation:
Trigonometric ratios
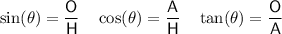
where:
 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
- H is the hypotenuse (the side opposite the right angle)
Part A
The slant height of the roof is the hypotenuse of a right triangle.
Considering the information given, use the cos trig ratio to determine the slant height.
A roof's base length is the distance from one corner of the roof to the other. Therefore, the base length of the given right triangle is half the roof base length.
Given:
 = 65°
= 65°- A = Half of roof base length = 6 ÷ 2 = 3 m
- H = Slant height
Substituting the given values into the formula and solving for H:
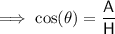
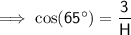
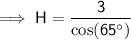
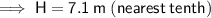
Part B
The slant height of the roof is the hypotenuse of a right triangle.
Considering the information given, use the cos trig ratio to determine the slant height.
A roof's base length is the distance from one corner of the roof to the other. Therefore, the base length of the given right triangle is half the roof base length.
Given:
 = 65°
= 65°- A = Half of roof base length = 9.6 ÷ 2 = 4.8 m
- H = Slant height
Substituting the given values into the formula and solving for H: