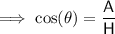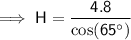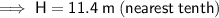Question

Please help with this question. 100 points!! I know it is a little long but I could really use the help.

The owners of the resort want to expand and build a row of condos at the western base of the mountain. Because of the amount of snow, the area gets most winters, it is important to have the pitch (steepness) of the roof of each condo at least 60°. To make the condos appealing to skiers and boarders, they want to model the condos after their cabins, but on a larger scale. The cabins have an A-line roof that forms an isosceles triangle as shown, with the base angles at 65° . The base length is 6m. Note: the slant height is the length of the side of the roof. (Picture Below)

Answer 1

A) 7.1 m

B) 11.4 m

Explanation:

Trigonometric ratios

`\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)`

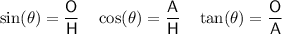
where:

• 
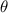  `\theta` is the angle
• O is the side opposite the angle
• A is the side adjacent the angle
• H is the hypotenuse (the side opposite the right angle)

Part A

The slant height of the roof is the hypotenuse of a right triangle.

Considering the information given, use the cos trig ratio to determine the slant height.

A roof's base length is the distance from one corner of the roof to the other. Therefore, the base length of the given right triangle is half the roof base length.

Given:

• 
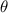  `\theta` = 65°
• A = Half of roof base length = 6 ÷ 2 = 3 m
• H = Slant height

Substituting the given values into the formula and solving for H:

`\sf \implies\cos(\theta)=(A)/(H)`

`\sf \implies\cos(65^(\circ))=(3)/(H)`

`\sf \implies H =(3)/(\cos(65^(\circ)))`

`\implies \sf H=7.1 \: m \: (nearest\:tenth)`

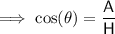
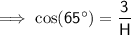
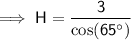
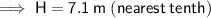
Part B

The slant height of the roof is the hypotenuse of a right triangle.

Considering the information given, use the cos trig ratio to determine the slant height.

A roof's base length is the distance from one corner of the roof to the other. Therefore, the base length of the given right triangle is half the roof base length.

Given:

• 
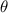  `\theta` = 65°
• A = Half of roof base length = 9.6 ÷ 2 = 4.8 m
• H = Slant height

Substituting the given values into the formula and solving for H:

`\sf \implies\cos(\theta)=(A)/(H)`

`\sf \implies\cos(65^(\circ))=(4.8)/(H)`

`\sf \implies H =(4.8)/(\cos(65^(\circ)))`

`\implies \sf H=11.4 \: m \: (nearest\:tenth)`

Answer 2

Required Formula

`\sf cos(x) = (adjacent)/(hypotenuse)`

Part A

Given: base length: 6m, half base: 3m, angle: 65°, let hypotenuse: h

Hence solve,

`\rightarrow \sf cos(x) = (a)/(h)`

`\rightarrow \sf cos(65) = (3)/(h)`

`\rightarrow \sf h = (3)/(cos(65))`

`\rightarrow \sf h =7.0986\ \approx \ 7.1 \ m`

The slant height is 7.1 meters when base length is 6 meter.

Part B

Given: base length: 9.6m, half base: 4.8m, angle: 65°, let hypotenuse: n

Hence solve,

`\rightarrow \sf cos (x) = (a)/(n)`

`\rightarrow \sf cos (65) = (4.8)/(n)`

`\rightarrow \sf n = (4.8)/(cos (65))`

`\rightarrow \sf n = 11.357 \ \approx \ 11.4 \ m`

The slant height is 11.4 meters when base length is 9.6 meter.