Answer:
![([(9-2)^(2)]^(4))/((4+3)^(5) )](https://img.qammunity.org/2021/formulas/mathematics/high-school/w16jpst2lesh20txpq5za7sl9dxol78u5l.png) = 7³
= 7³
Explanation:
Let us revise some rules of exponents
Let us use some of these rules to solve the question
∵ The expression is
![([(9-2)^(2)]^(4))/((4+3)^(5) )](https://img.qammunity.org/2021/formulas/mathematics/high-school/w16jpst2lesh20txpq5za7sl9dxol78u5l.png)
→ At first, simplify the bracket
∵ 9 - 2 = 7 and 4 + 3 = 7
∴
![([(9-2)^(2)]^(4))/((4+3)^(5) )](https://img.qammunity.org/2021/formulas/mathematics/high-school/w16jpst2lesh20txpq5za7sl9dxol78u5l.png) =
=
![([(7)^(2)]^(4))/((7)^(5) )](https://img.qammunity.org/2021/formulas/mathematics/high-school/j2h61zu0j1oqui8s78fhr1kquz7uv35hwo.png)
→ Use the 3rd rule above to simplify the numerator
∵
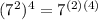
∴
![([(7)^(2)]^(4))/((7)^(5) )](https://img.qammunity.org/2021/formulas/mathematics/high-school/j2h61zu0j1oqui8s78fhr1kquz7uv35hwo.png) =
=
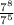
→ Use the 2nd rule above to simplify the result
∴
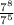 =
=
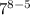 = 7³
= 7³
∴
![([(9-2)^(2)]^(4))/((4+3)^(5) )](https://img.qammunity.org/2021/formulas/mathematics/high-school/w16jpst2lesh20txpq5za7sl9dxol78u5l.png) = 7³
= 7³